Mesh Edit
geometric mesh operations
In this project:
- Evaluating Bezier curves and surfaces with de Casteljau subdivision
- Implementing mesh operations: edge flips and splits
- Upsampling meshes with loop subdivision
Section I: Bezier Curves and Surfaces
Part 1: Bezier Curves with 1D de Casteljau Subdivision
de Casteljau’s algorithm is a recursive method for evaluating Bezier curves. Given \(t\), a parameter that varies from zero to one, and \(n\) control points, one iteration of de Casteljau’s algorithm will calculate the next \(n - 1\) intermediate control points by using linear interpolation between every pair of consecutive control points. Given two control points \(p_{0}\) and \(p_{1}\) and a value for \(t\), we can calculate the weighted average as \((1 - t) \cdot p_{0} + t \cdot p_{1}\)
This sequence shows six levels of Bezier curve evaluation, from the original control points down to the final evaluated point and the complete Bezier curve.
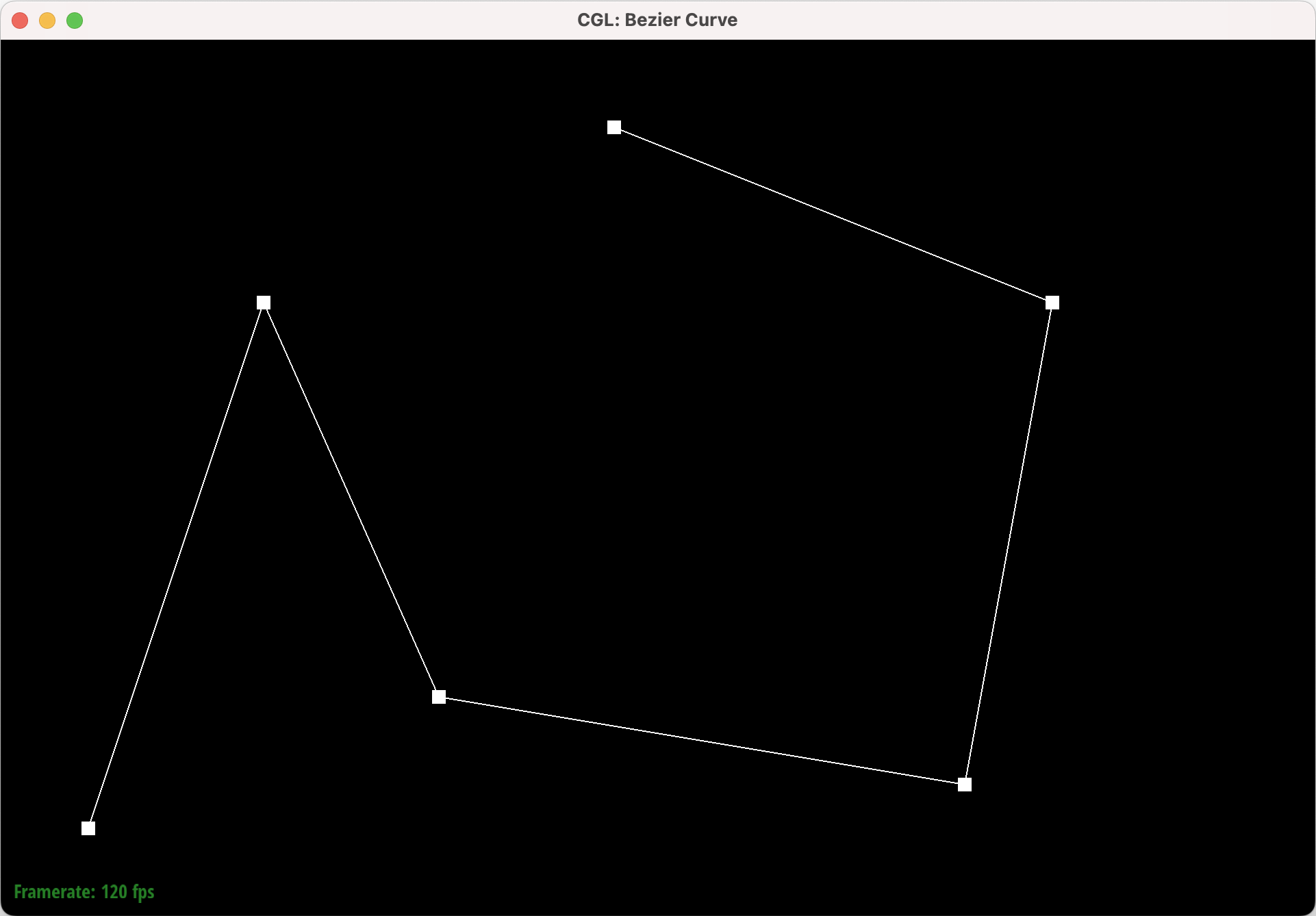
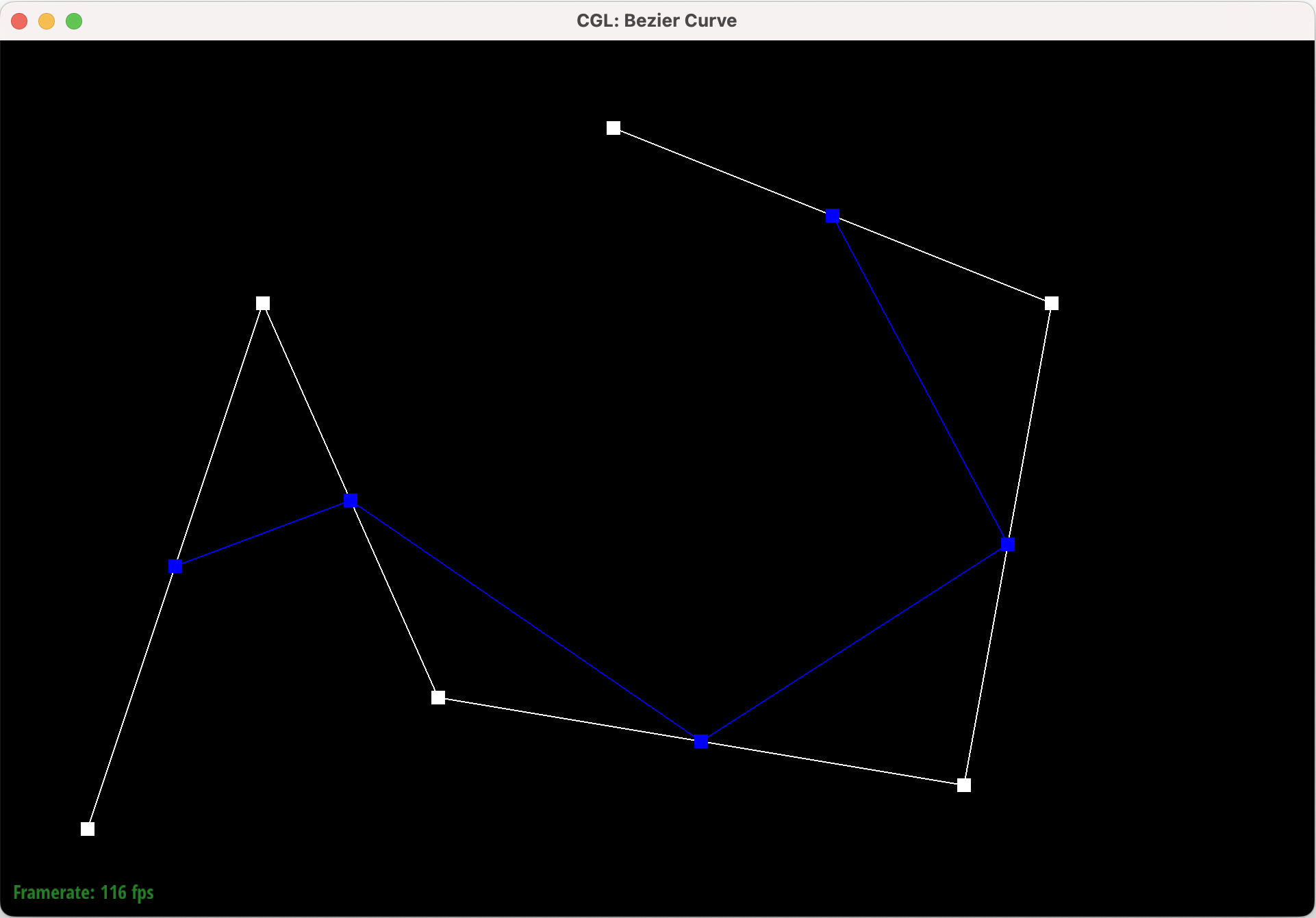


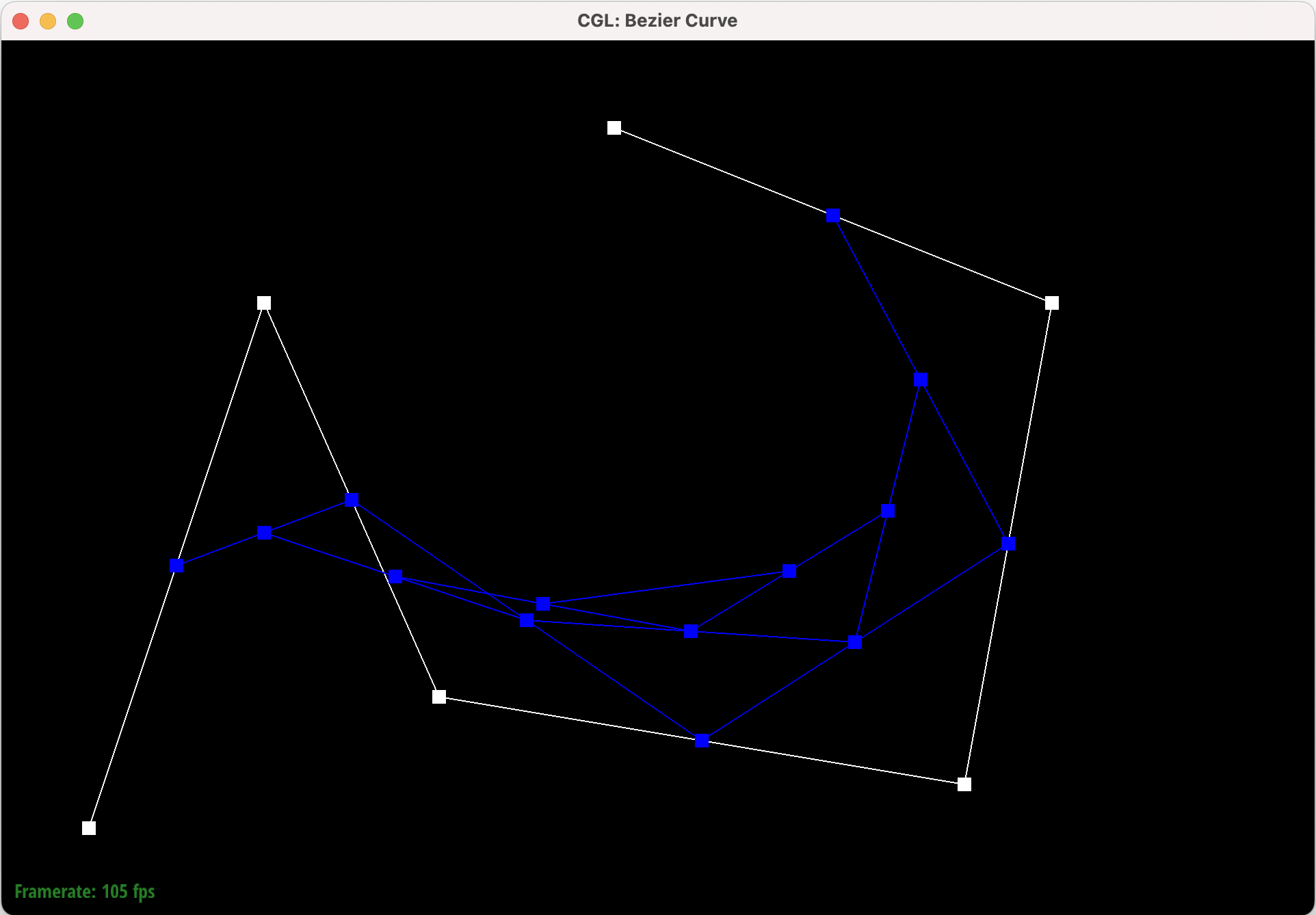

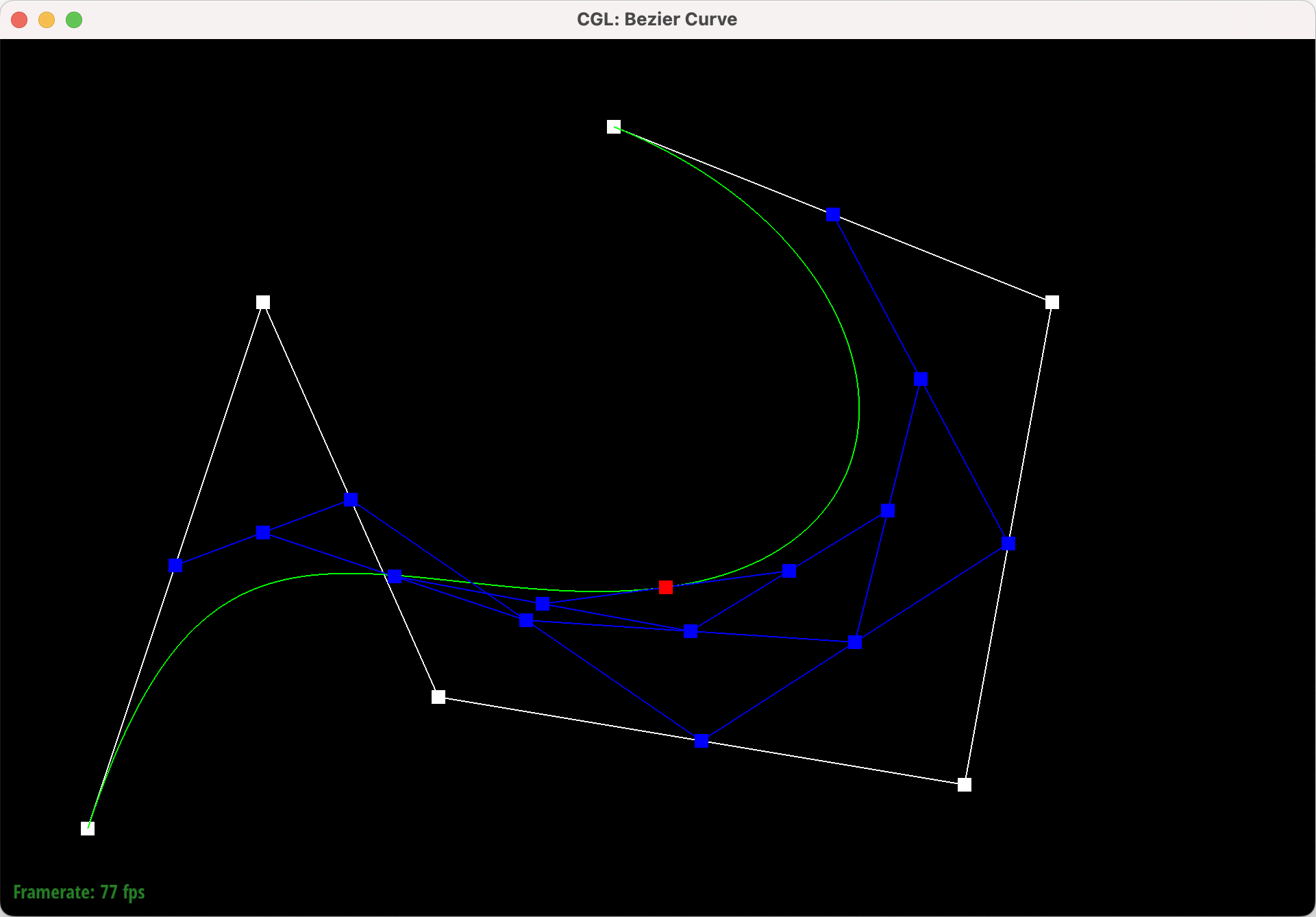
Part 2: Bezier Surfaces with Separable 1D de Casteljau
Given an \(n \times n\) grid of control points, we can use the separable application of de Casteljau’s algorithm along the two different axes to evaluate the points of a Bezier surface.

Section II: Triangle Meshes and the Half-Edge Data Structure
Part 3: Area-Weighted Vertex Normals
For a vertex in a geometric mesh, we calculate its area-weighted vertex normal as the normalized average of the surface normal vectors of the vertex’s surrounding faces, where each surface normal vector is weighted by the area of its face. We can use these area-weighted vertex normals for Phong shading.
Part 4: Edge Flips
An edge flip is a basic topological operation. To implement edge flips, I identify all elements in the original mesh of a pair of triangles: \(6\) half-edges, \(2\) faces, \(5\) edges, and \(4\) vertices. If either of the neighboring faces are boundary faces, I immediately return the given edge. Otherwise, I re-assign the half-edges of each vertex, edge, and face in the modified mesh. Finally, I set all the neighbors of each of the \(6\) half-edges. Finally, I return the new flipped edge by accessing the corresponding edge of one of its two half-edges.
Part 5: Edge Splits
Edge splits are another basic topographical operation. To perform an edge split, I list out all the half-edges, vertices, edges, and faces that are present in the original mesh of a pair of triangles. During any type of edge split, I never delete any existing mesh elements. To split a regular, non-boundary edge, I reassign pointers of the original elements if necessary, and create \(1\) new vertex called \(M\), \(6\) new half-edges, \(3\) new edges, and \(2\) new faces. Then, I set the half-edges of each vertex, edge, and face in the new mesh. Finally, I set all the neighbors of each half-edge in the new mesh.
Splitting boundary edges requires a slightly different implementation. As before, I list out the existing elements in the original mesh, including a pointer to the virtual boundary face. Then, to perform the edge split operation, I create \(1\) new vertex called \(M\), \(4\) new half-edges (one of which is a boundary half-edge), \(2\) new edges (one of which is a boundary edge), and \(1\) new face. I do not divide the virtual boundary face or create any new virtual boundary faces. Then, I set the half-edges of each element and set the neighbors of each half-edge in the new mesh. However, ordering matters when setting the neighbors of the two boundary half-edges, since I need to access the next boundary half-edge before “losing” the pointer during reassignment.
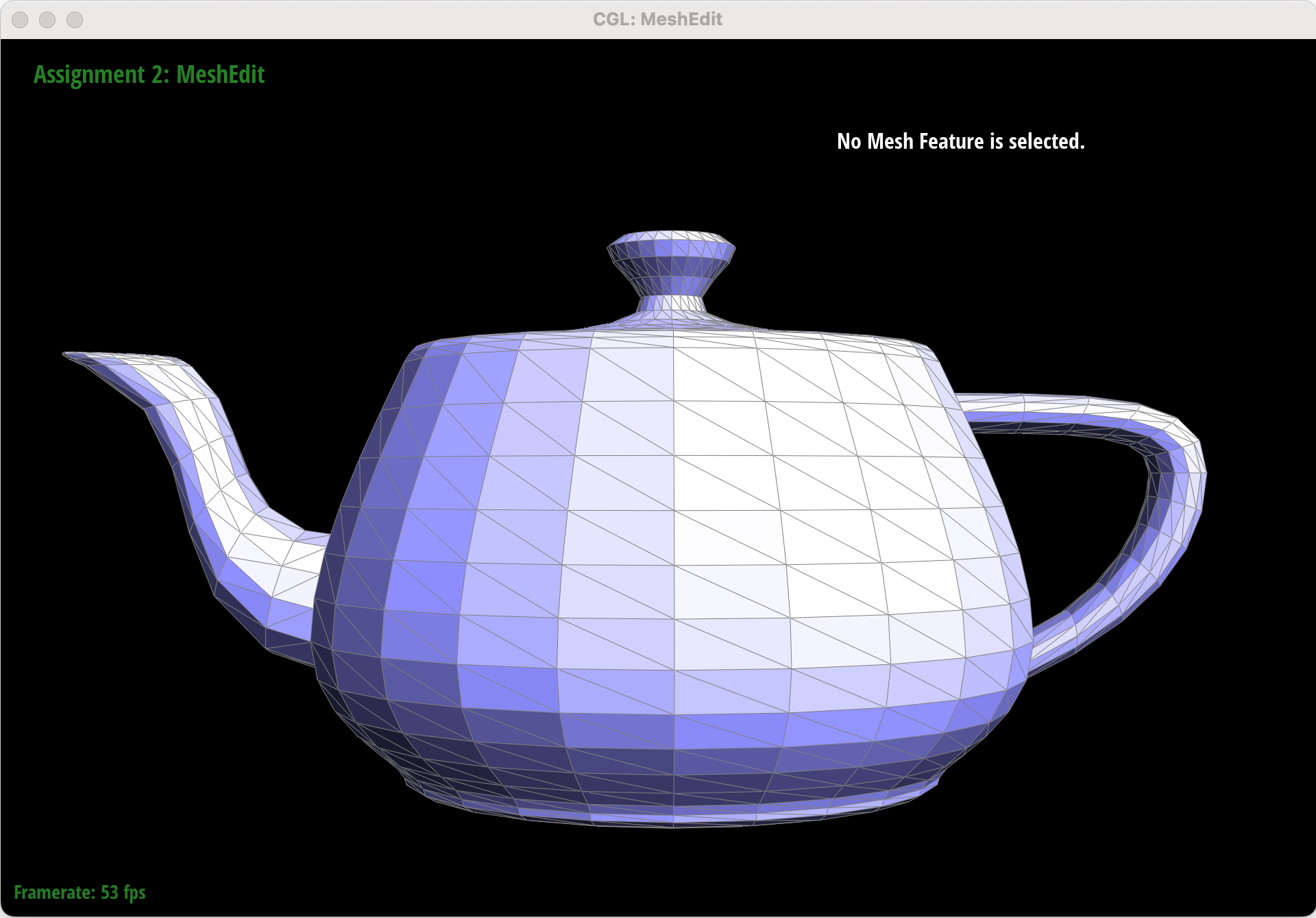
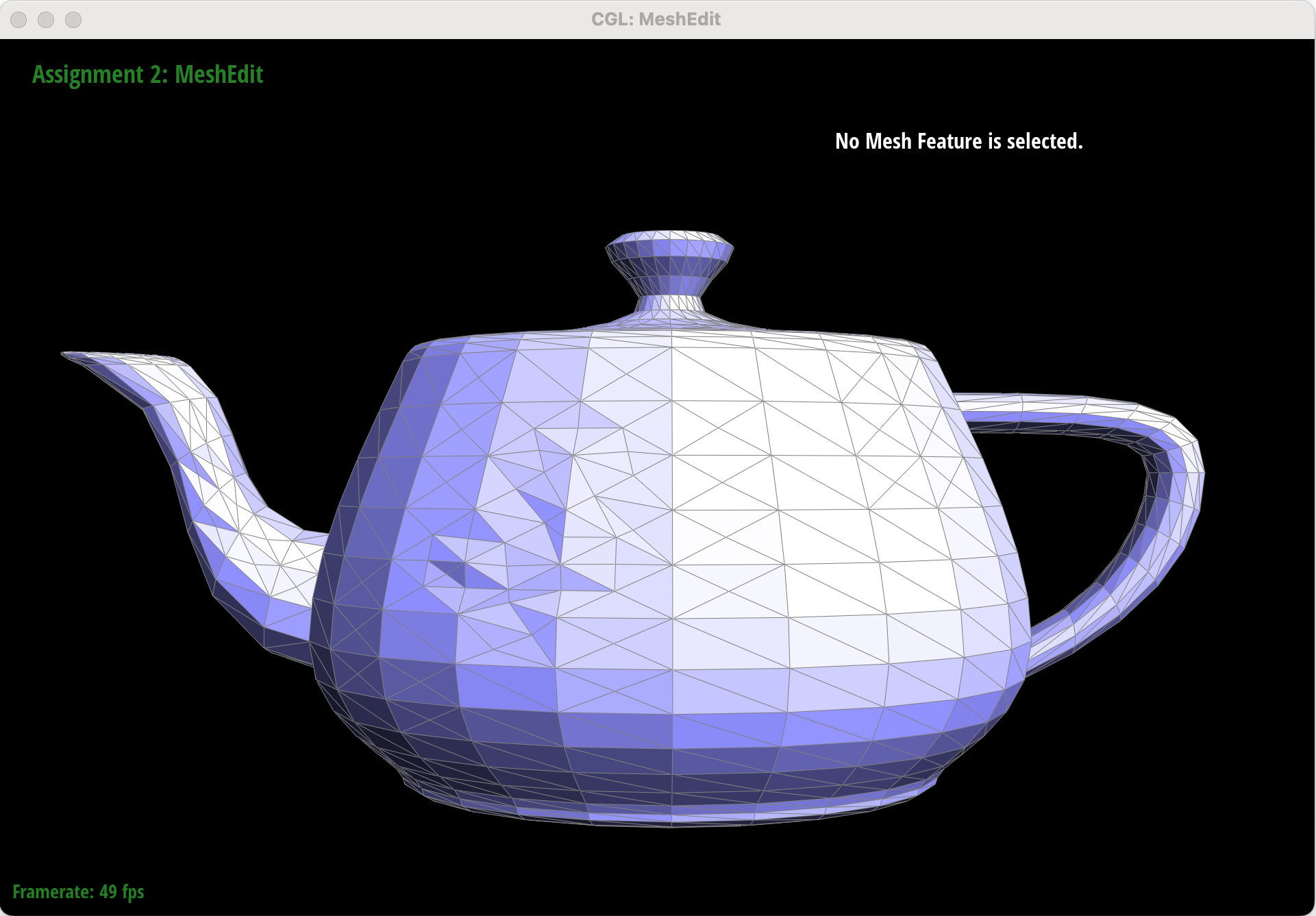

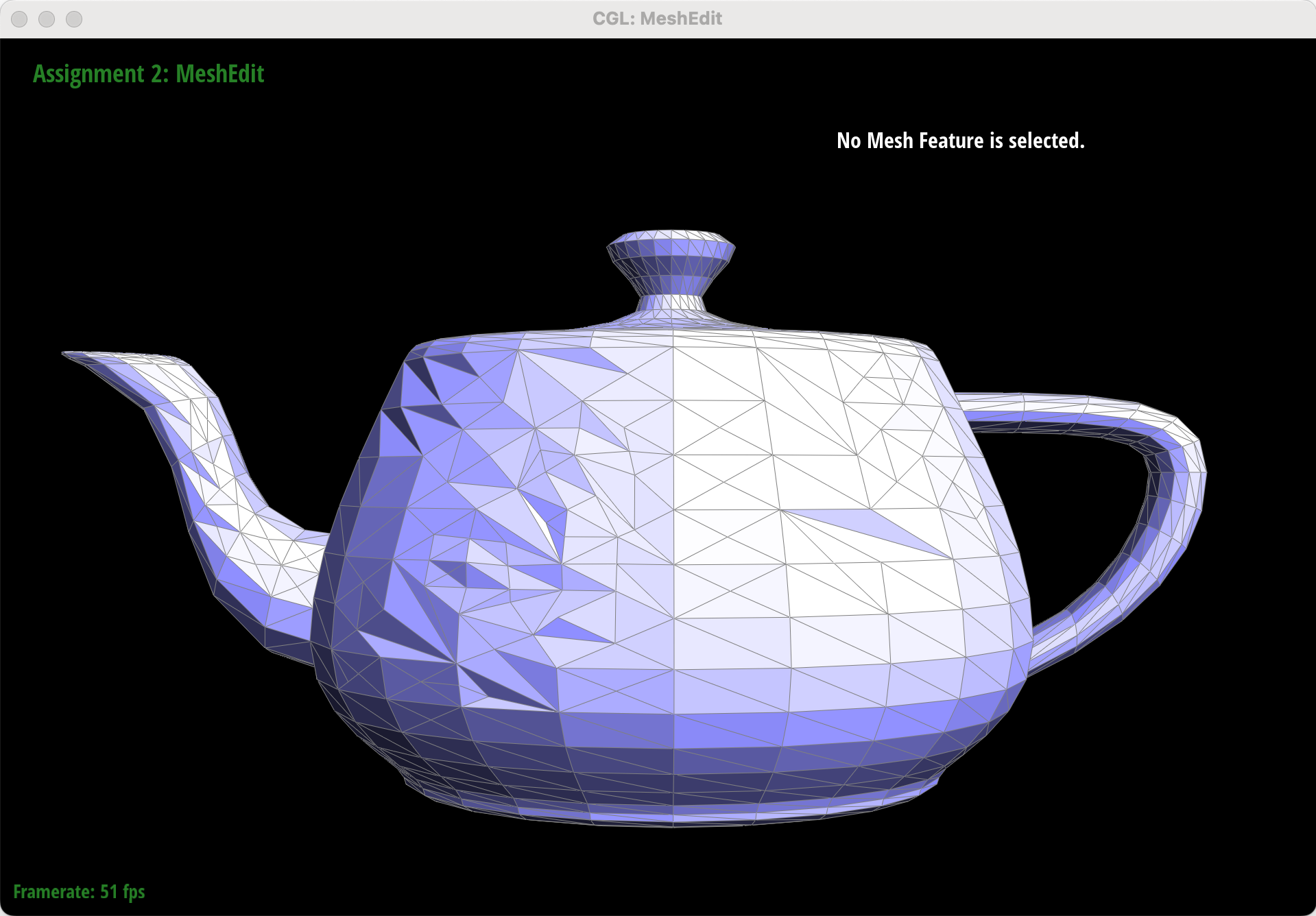
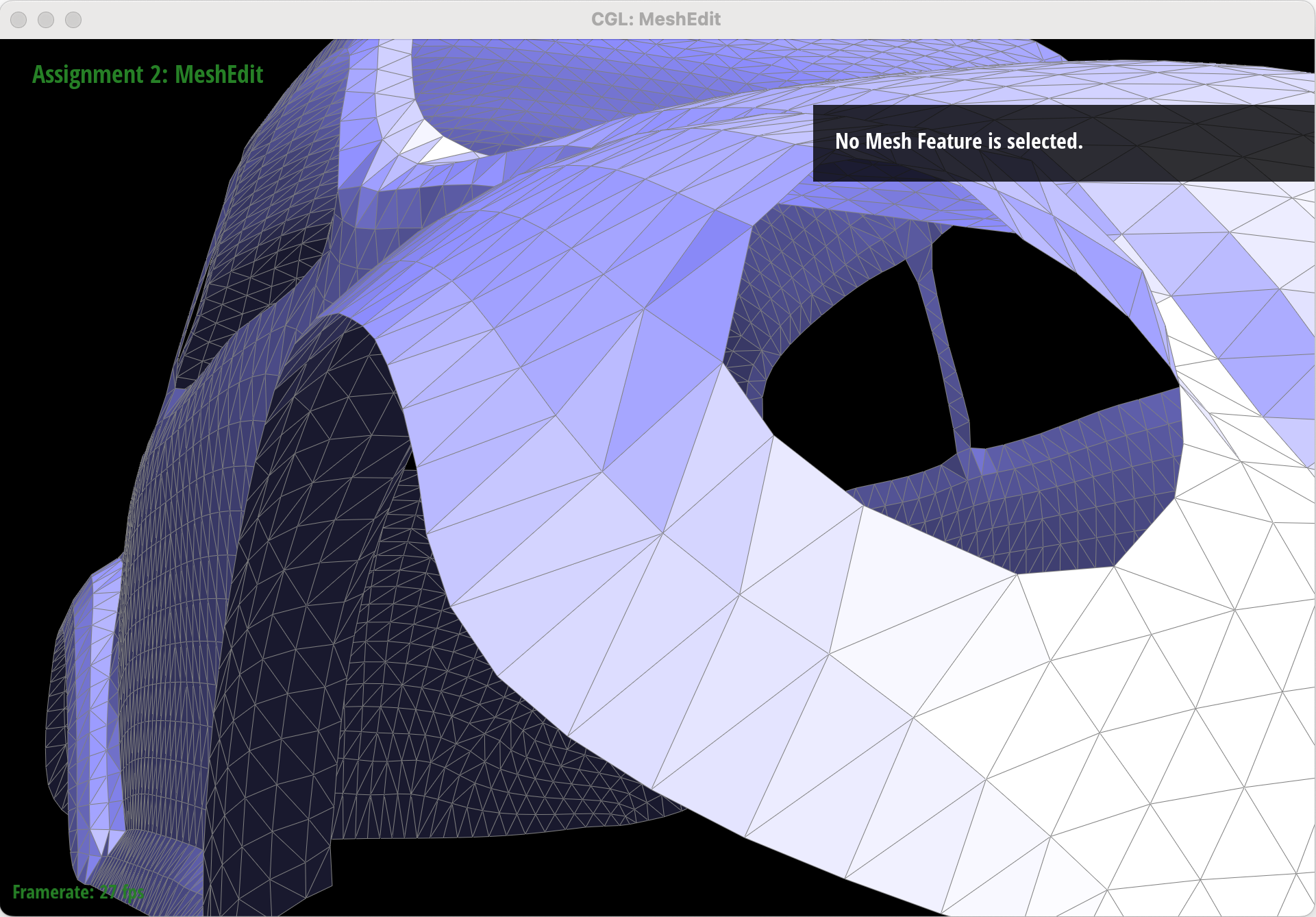
Part 6: Loop Subdivision for Mesh Upsampling
To implement loop subdivision, I iterate over all vertices in the original mesh and calculate each vertex’s updated position. Then, I calculate the position of the new vertex associated with every edge in the original mesh that will be added in the process of loop subdivision. I split each original edge; since new edges are appended to the end of the list of edges, I determine the number of edges in the original mesh and iterate through that number of edges so that I only split original edges. After splitting edges, I iterate over all edges in the edited mesh and flip any edge that connects an old vertex to a new vertex.
After loop subdivision, sharp corners and edges in the original mesh become smoothed out. The effect is more apparent if the original mesh is relatively low-poly.







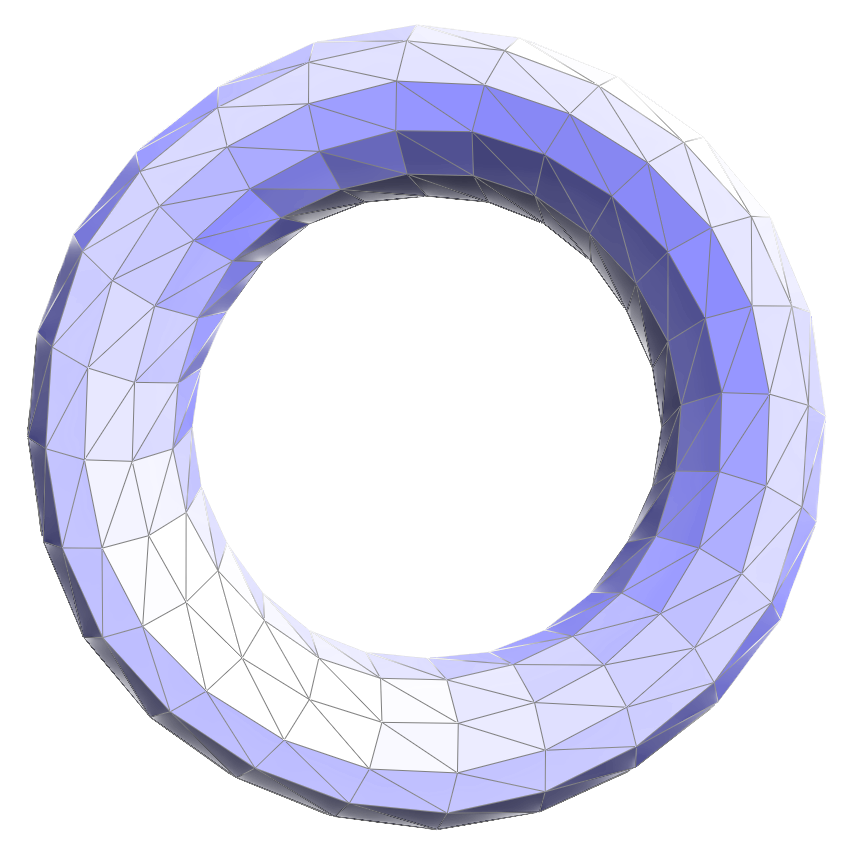
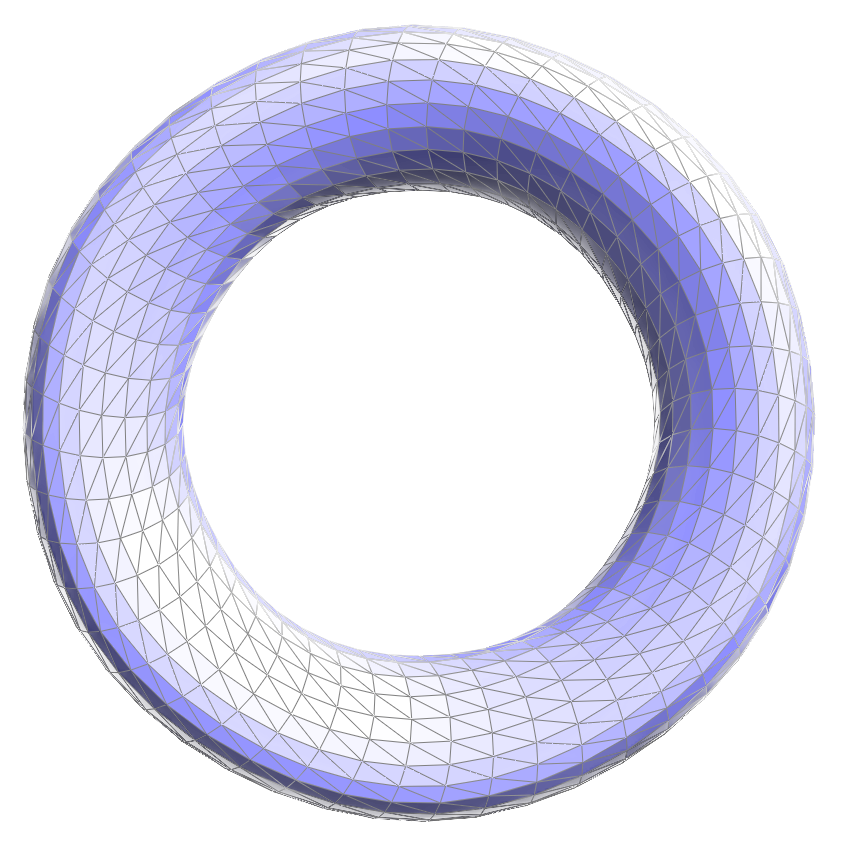
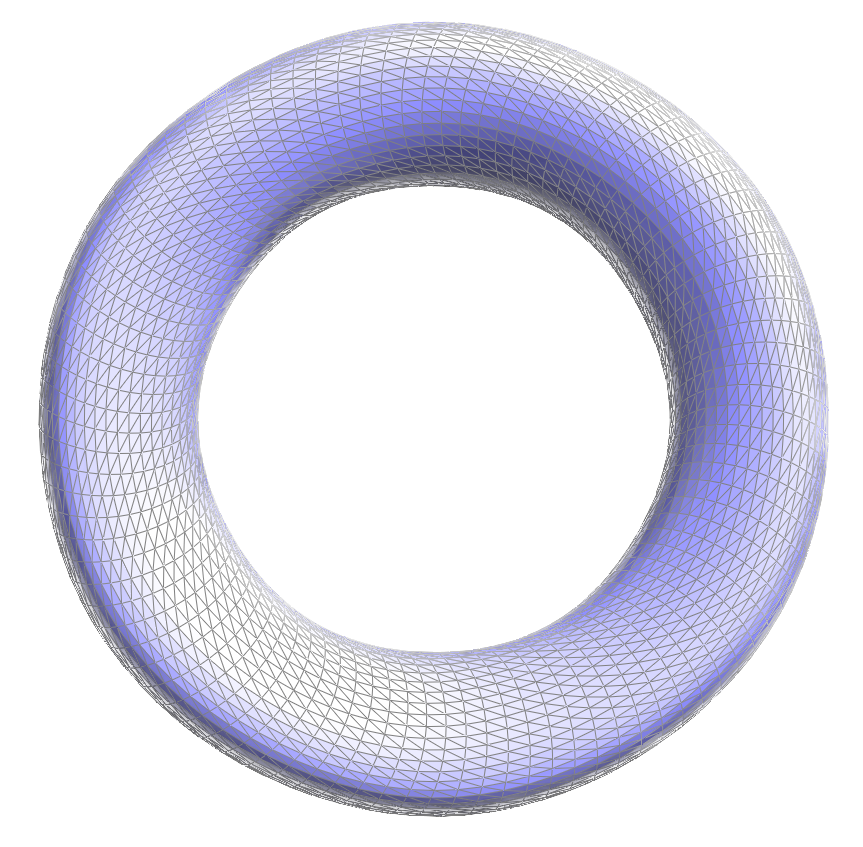
This smoothing effect can be reduced by pre-splitting some edges.




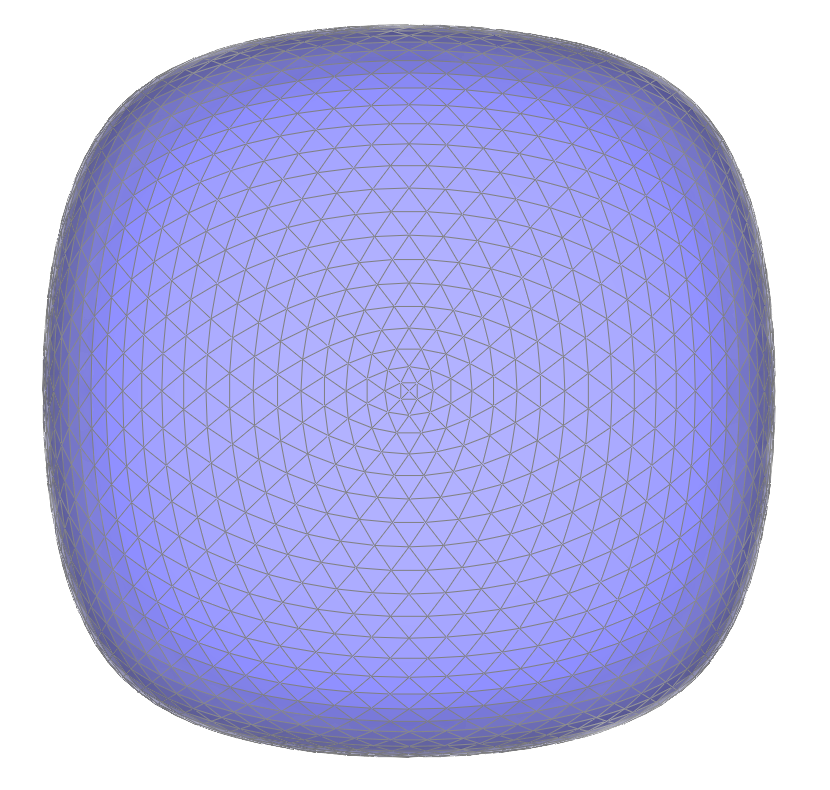

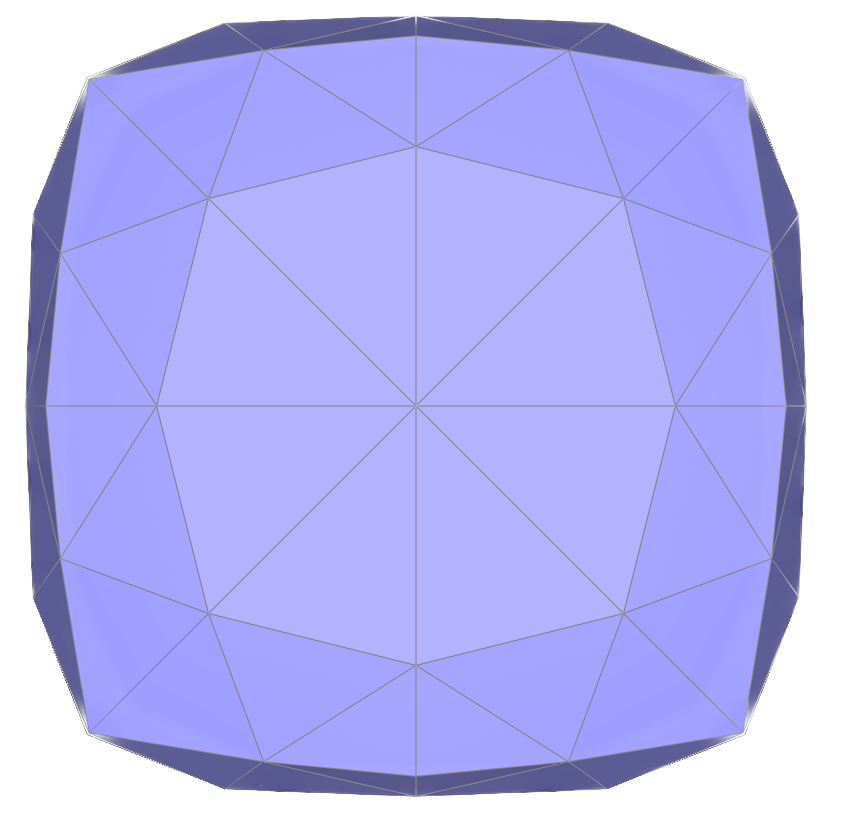


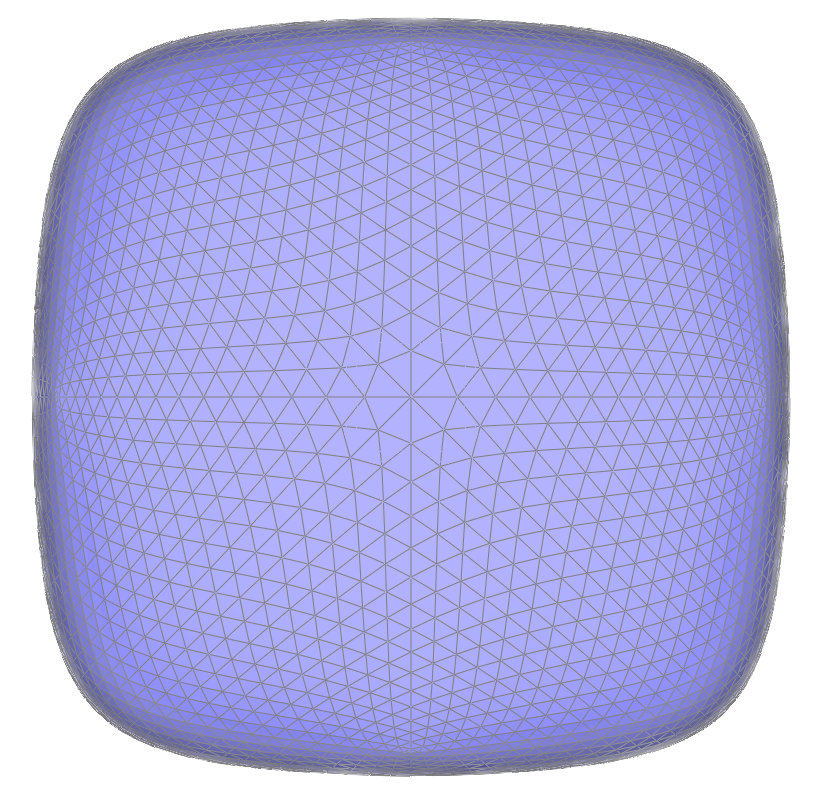
However, if the topology of the original is not symmetrical, the mesh can become asymmetrical with upsampling.




